Bir Kürenin Hacmini Hesaplama

Bir Kürenin Hacmini Hesaplama, bu ihtiyacın oluşması durumunda Excel üzerinden Pİ formülü ile nasıl hesaplama yapılacağını öğretmektedir.

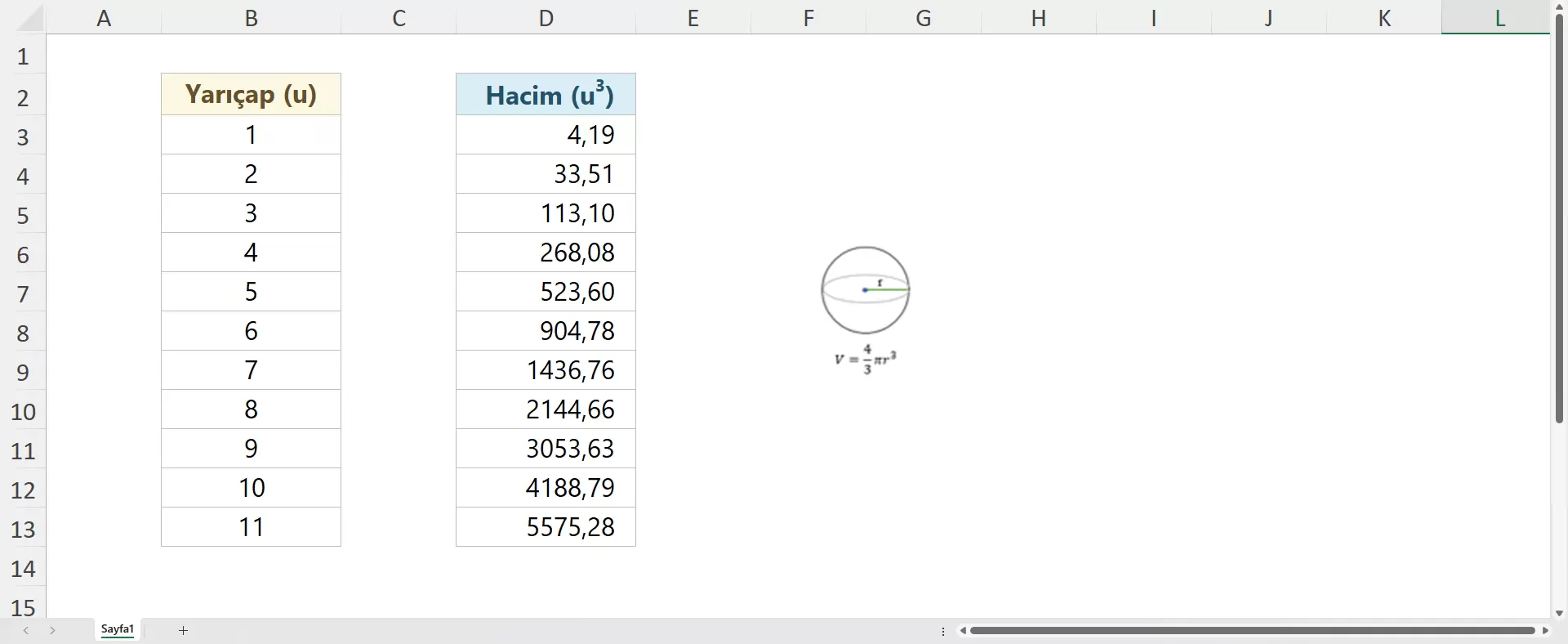
Bir Kürenin Hacmini Hesaplama – Kürenin Tanımı

Matematik ve fizikte sıkça karşılaşılan temel bir konudur. Küre, her noktası merkeze eşit uzaklıkta olan üç boyutlu bir cisimdir. Homojen bir yüzeye sahip olan küre, geometride önemli bir yer tutmaktadır. Bu nedenle, üç boyutlu alan hesaplamalarında küre formülü temel alınmaktadır. Bu formül, bir kürenin sahip olduğu hacmi bulmamızı sağlamaktadır. Hacim, bir cismin uzayda kapladığı alanı ifade etmektedir. Böylece, küre için bu, içindeki boşluğun büyüklüğünü belirtmektedir. Ayrıca, kürenin hacmini hesaplamak için kullanılan formül ise V=34​πr3 olarak gösterilmektedir. Çünkü, bu formülde ‘V’ hacmi, ‘r’ ise kürenin yarıçapını temsil etmektedr. Yarıçap, kürenin merkezinden yüzeyine olan uzaklıktır. Ayrıca, hacim hesaplamasının anahtar bileşenidir. Dolayısıyla, formüldeki r3 ifadesi, yarıçapın küpünün alınması gerektiğini belirtmektedir. Bu nedenle, hacmin yarıçapla orantılı olarak çok daha hızlı büyüdüğünü göstermektedir. π (pi) sayısı, dairenin çevresinin çapına oranıdırç. Çünkü, küresel hesaplamaların vazgeçilmez bir parçasıdır.

Bu formülü kullanarak, bilinen bir kürenin hacmini kolayca hesaplanmaktadır. Buna bağlı olarak, fiziksel dünyadaki birçok sorunun çözülmesi de kolaylaşmaktadır. Örneğin, bir topun ne kadar hava alacağını veya bir balonun ne kadar su taşıyabileceğini bu formülle bulunabilmektedir. Bu basit ancak güçlü formül, mimariden astronomiye kadar pek çok alanda pratik uygulamalara sahiptir.

Küre Hacim Formülü

Kürenin hacmini hesaplamak için ( V = frac{4}{3} pi r^3 ) formülü kullanılmaktadır. Bu formül, kürenin yarıçapı (r) bilindiğinde, uzayda kapladığı alanı yani hacmini bulmamızı sağlamaktadr. Bu sayede, topun içine ne kadar hava sığdığı veya bir balonun kaç litre su taşıyabileceği gibi sorulara kolayca yanıt bulunmaktadı. Bu basit ama etkili formül, fiziksel dünyanın birçok problemine pratik çözümler sunmaktadır.

• Burada ( V ) kürenin hacmini,
• ( r ) kürenin yarıçapını,
• ( pi ) ise matematiksel sabiti (yaklaşık 3.14159) temsil etmektedir.
• Bu formül, kürenin tüm boyutlarını dikkate alarak hacmini vermektedir.
• Yarıçap bilindiği sürece hacim kolayca hesaplanmaktadır.

Bu formül, küre gibi düzgün yüzeyli cisimler için idealdir.

Bir Kürenin Hacmini Hesaplama Adımları

Hacim hesaplama, belirli adımlar izlenerek yapılmaktadır. Bu adımların ilki, hesaplama yapılması istenen kürenin yarıçapını doğru bir şekilde ölçmektir. Ardından, bu yarıçap değerini V=34​πr3 formülündeki ‘r’ yerine koyarak işlemi tanımlanmaktadır. Son olarak, elde edilen sonuç, kürenin hacmini vermektedir. Bu sayede, hacimle ilgili her türlü problemi çözülmektedir.

• Önce kürenin yarıçapı ölçülmektedir.
• Yarıçap küp ile çarpılmaktadır (( r^3 )).
• Sonuç ( pi ) ile çarpılarak dörtte üçü alınmaktadır.
• Elde edilen sonuç, kürenin hacmidir.

Bu adımlar, kürenin hacmini bulmak için uygulanmaktadır.

Yaygın Kullanım Alanları

Küre hacmi hesaplamaları pek çok alanda kullanılmaktadır.

• Mühendislikte malzeme miktarını belirlemede,
• Eğitimde öğretim materyali olarak,
• Bilimde atom ve moleküllerin boyutlarını anlamada,
• Sanatta eserlerin boyut ve oranlarını ayarlamada kullanılmaktadır.

Küre hacmi, teorik ve pratik pek çok uygulamada önemlidir.

Hacim Hesaplama Örnekleri

Günlük yaşamda karşılaşılan hacim hesaplama örnekleri.

• Bir balonun içindeki hava miktarını hesaplama,
• Bir kavanoz içine konulabilecek miktarda malzeme ölçümü,
• Dekoratif eşyaların boyutlandırılması,
• Bilimsel deneylerde kullanılan malzemelerin ölçülmesi.

Bu örnekler, küre hacmi hesaplamasının pratik kullanımlarını göstermektedir.

Bir Kürenin Hacmini Hesaplama Dosyası Hakkında

Dosya formülle, bir kürenin hacmini hesaplamak için, üs operatörüyle (^) birlikte Pİ formülü kullanılabilmektedir. Geometride bir küre, üç boyutlu bir uzayda belirli bir noktadan aynı uzaklıkta (r) olan noktalar kümesi olarak tanımlanmaktadır. Bir kürenin hacmini hesaplamanın formülü şöyledir: Bu tanım, kürenin hacmini hesaplarken neden yarıçapın (r) ve π (pi) sayısının bu kadar önemli olduğunu açıklamaktadır. Çünkü, bu bilgiler ışığında, Excel’de bu formülü uygulamak, karmaşık hesaplamaları bile kolayca yapmanızı sağlamaktadır. Böylece, manuel hesaplamalara gerek kalmadan, sadece yarıçapı girerek kürenin hacmini anında bulabilirsiniz.

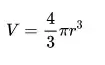
R yarıçapı temsil ettiğinde ve yunan harfi π ("pi") bir çemberin çevresinin çapına oranını temsil etmektedir. Excel‘de π, 3.14159265358979 sayısını 15 basamağa kadar veren PI işlevine sahip bir formülde temsil edilmektedir.

Bu tür bir ihtiyacı olanlar için örnek formülümüzü dosyamızdan inceleyebilirsiniz.